11289. Размеченные графы

Пусть количество вершин в графе равно n. Подсчитайте количество размеченных графов с n вершинами (размеченный означает, что вершины помечены числами от 1 до n). Ребра графов считаются неориентированными, а петли и кратные ребра запрещены.

Вход. Количество вершин n (1 ≤ n ≤ 10⁵) в графе.

Выход. Выведите количество размеченных графов с n вершинами. Выведите ответ по модулю 10⁹ + 7.

Пример входа 1	Пример выхода 1
2	2
Пример входа 2	Пример выхода 2
3	8

РЕШЕНИЕ

графы

Анализ алгоритма

В графе из n вершин можно провести p = n * (n – 1) / 2 ребер. Выбрав произвольное подмножество ребер, можно получить размеченный граф. Количество размеченных графов равно числу подмножеств всего множества возможных ребер, а именно 2^p.

Пример

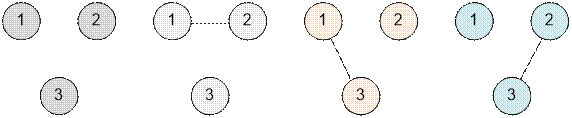
Для n = 2 имеются 2 графа. В первом графе ребра отсутствуют. Во втором графе присутствует единственное ребро.

Для n = 3 имеются 8 графов:

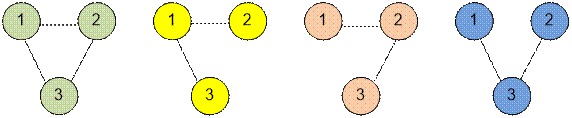
Реализация алгоритма

Функция PowMod вычисляет xⁿ mod m.

long long PowMod(long long x, long long n, long long m)

{

if (n == 0) return 1;

if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);

return (x * PowMod(x, n - 1, m)) % m;

}

Основная часть программы. Читаем входное значение n.

scanf("%lld", &n);

Вычисляем и выводим ответ res = mod (10⁹ + 7).

p = n * (n - 1) / 2;

res = PowMod(2, p, MOD);

printf("%lld\n", res);